√1000以上 三角形 辺の比 ��理 314098-三角形 辺の比 定���
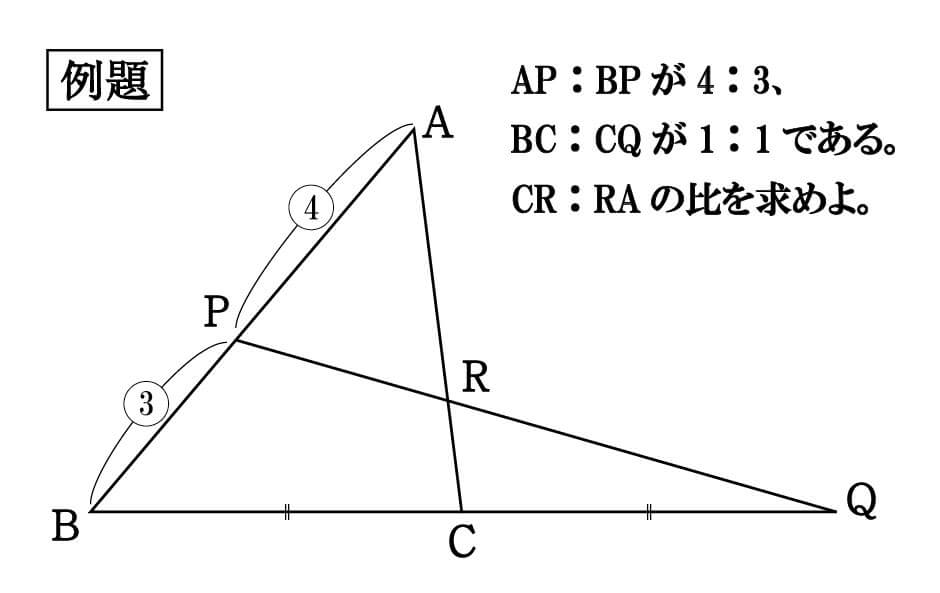
三角形 OAB において,辺 AB を 21 に内分する点を D とし,直線 OA に関して点 D と対称な点を E とする。$\overrightarrow{\text{OA}}=\vec{a},\overrightarrow{\tex mm参考書 高校数学の解法 共通テスト数学 共通テスト英語 共通テストリスニング 高校数学の解法 共通テスト数学 共通テスト英語 共通テスト
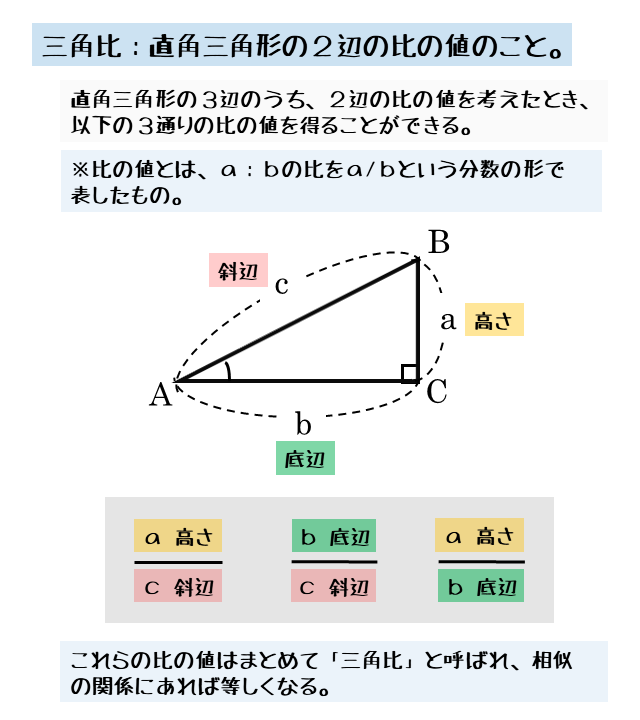
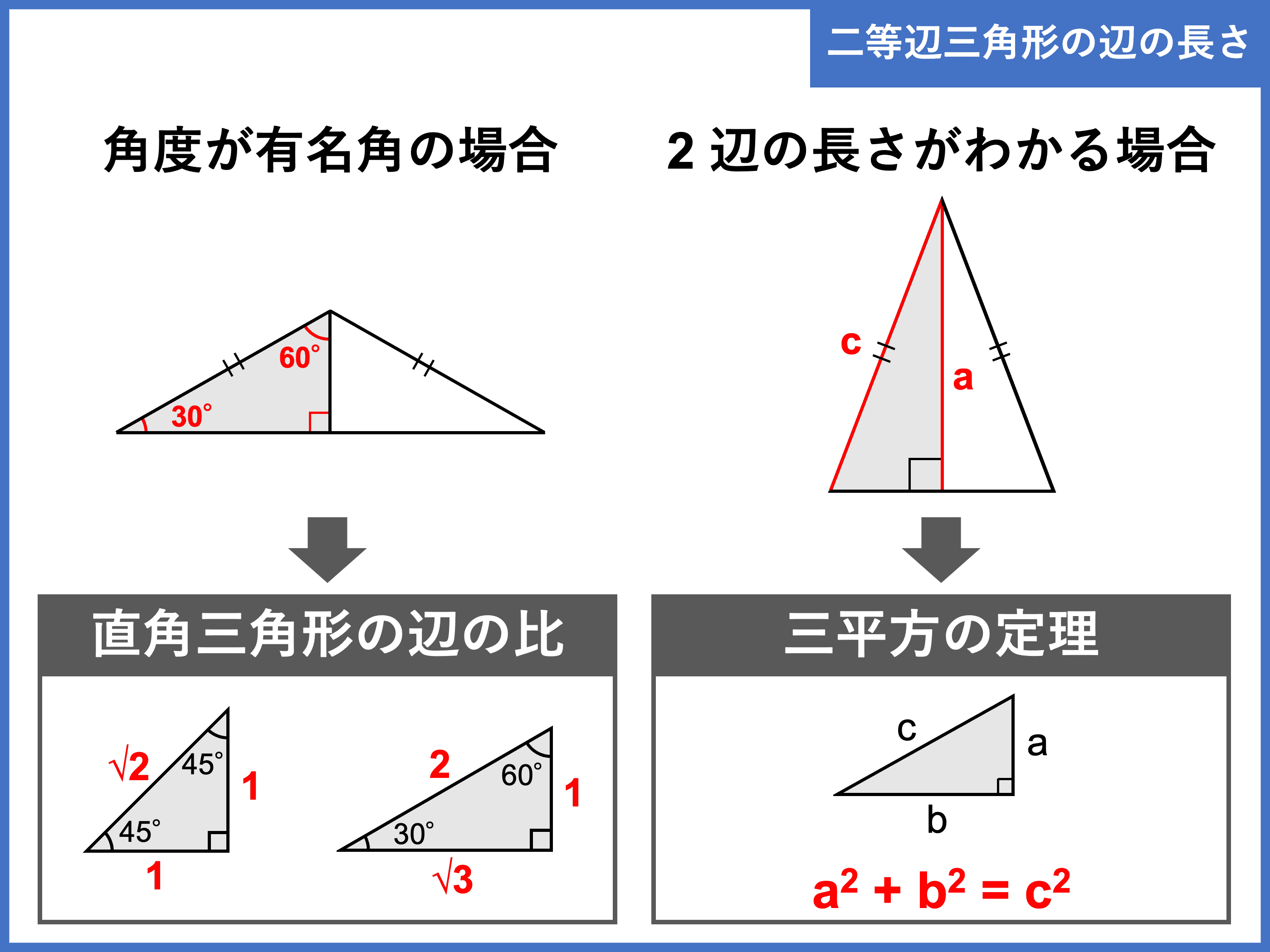
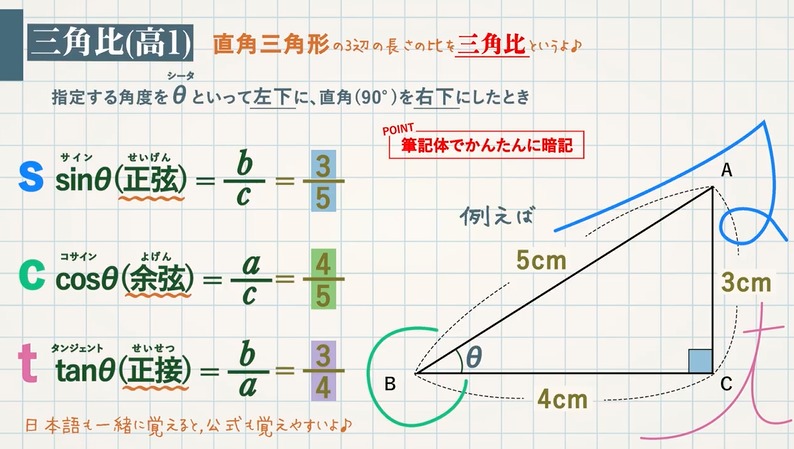
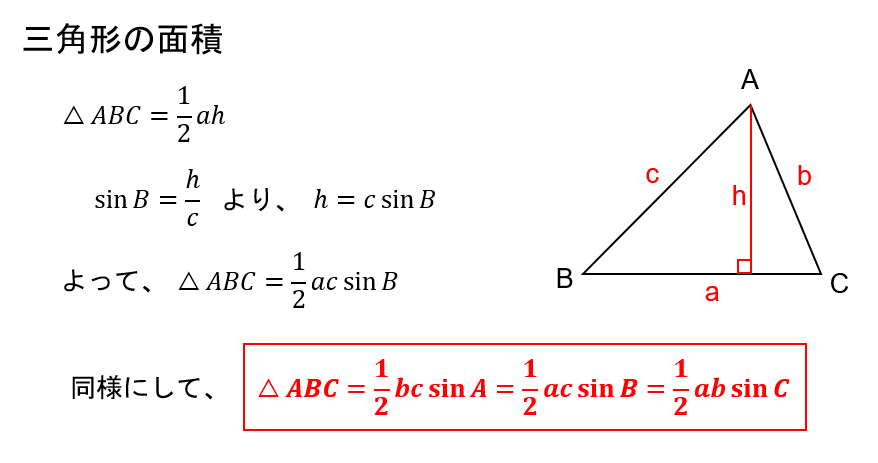
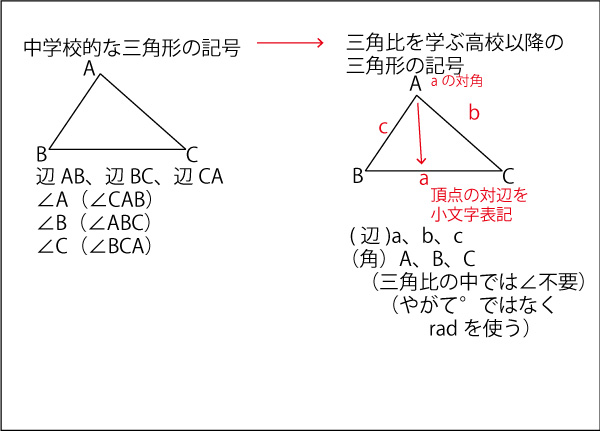
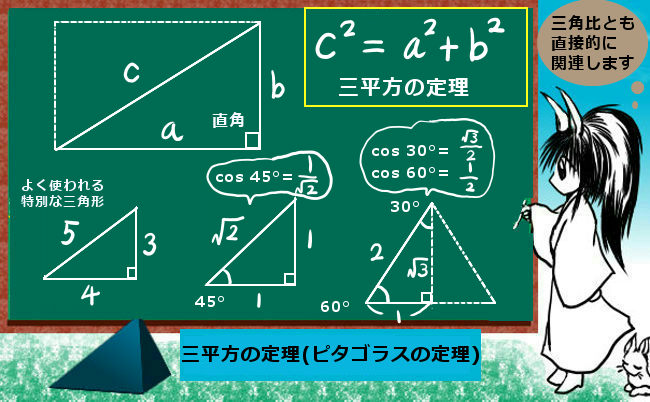
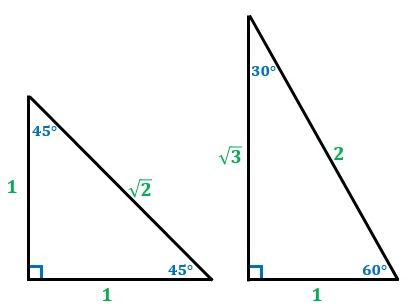
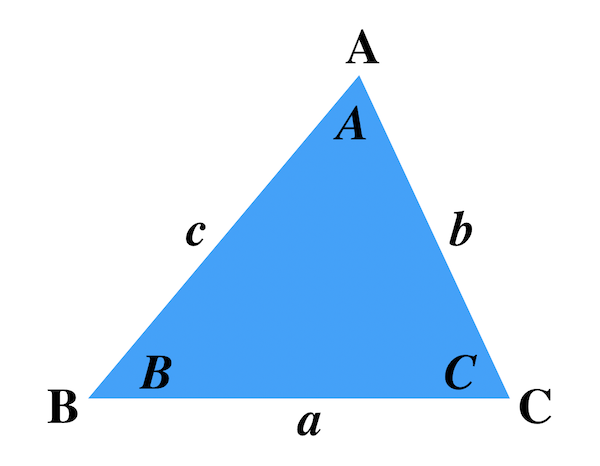
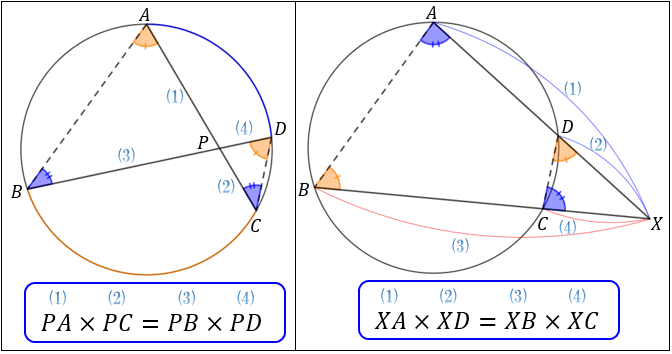
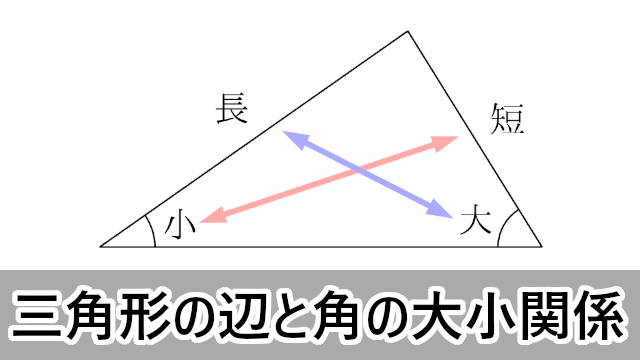
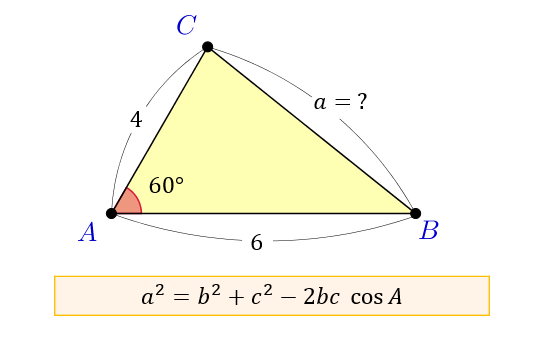
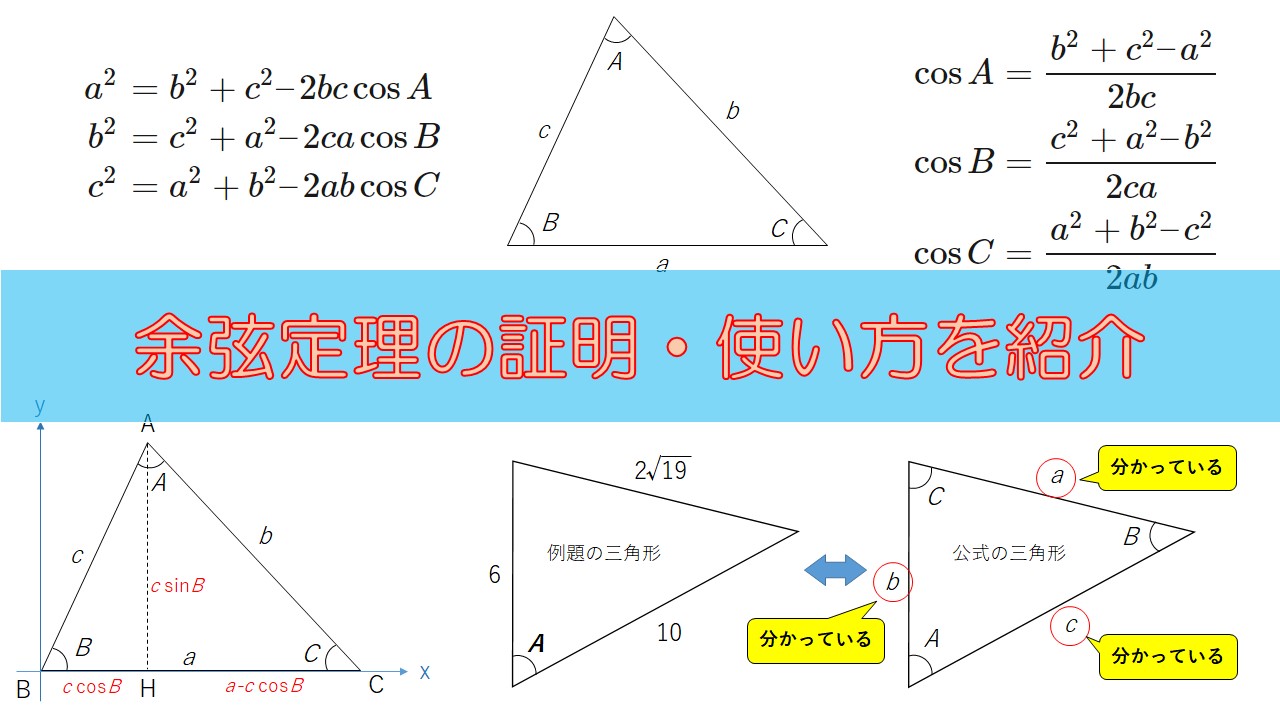
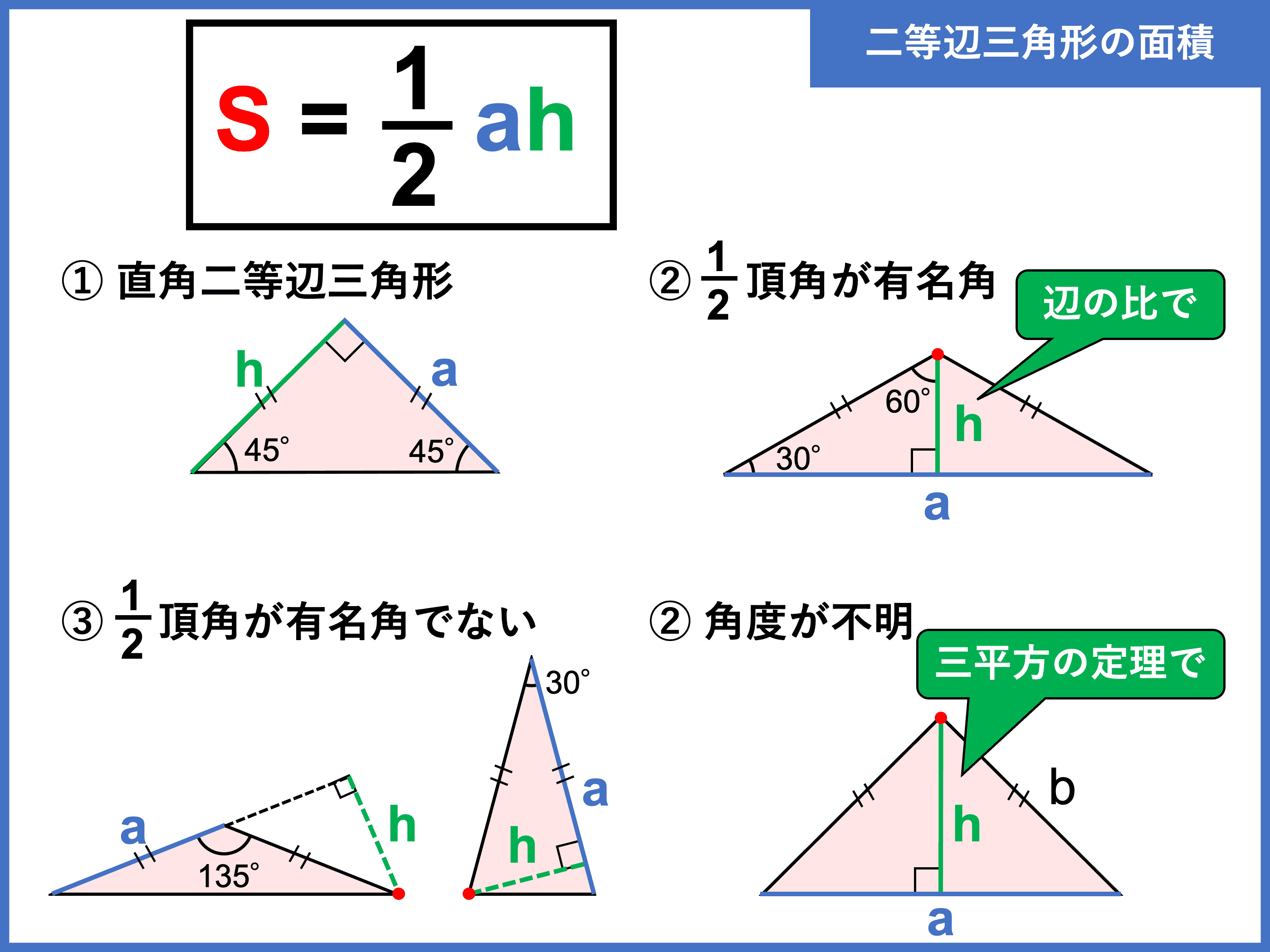
三角形 辺の比 定理-三角比を利用することによって、辺の長さ(または三角比の値)を求められる公式が正弦定理と余弦定理です。 正弦定理と余弦定理は「わからない辺の長さや角度を計算できる」という点では同じです。 ただ、使用する場面が異なります。 正弦定理を利用するべき計算があれば、余弦定理を利用して計算するべき場面もあるのです。 これらの公式を理解した後 つまり、内角がそれぞれ90°、45°、45°の二等辺三角形の三辺の比は、1:1:√2となるのです。 公式 直角二等辺三角形の辺の長さの比:1:1:√2 この公式はかなりの頻度で利用する必要が生まれますので、是非とも覚えてしまうことをおすすめします。
三角形 辺の比 定理のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「三角形 辺の比 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  |  |
「三角形 辺の比 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 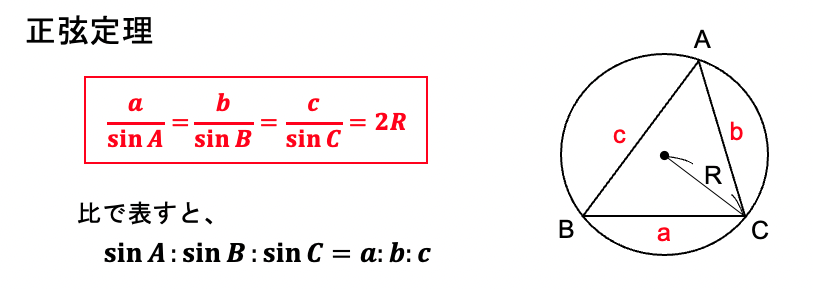 |  |
 |  |  |
 |  |  |
 |  | |
「三角形 辺の比 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  |  |
「三角形 辺の比 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 |  |  |
「三角形 辺の比 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 |  | |
「三角形 辺の比 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  | |
「三角形 辺の比 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  |  |
 |  |  |
「三角形 辺の比 定理」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
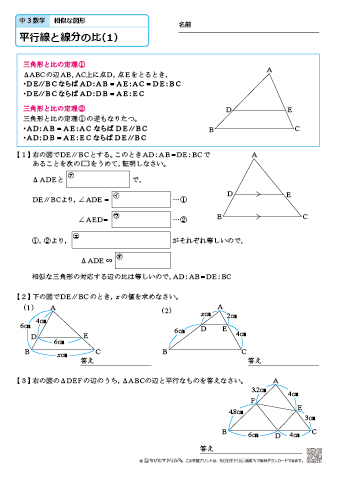 | 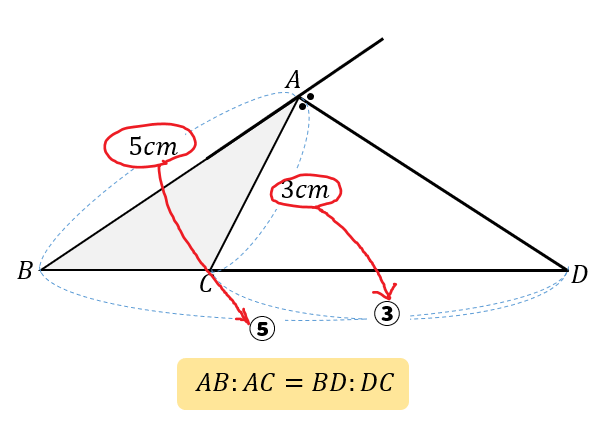 |
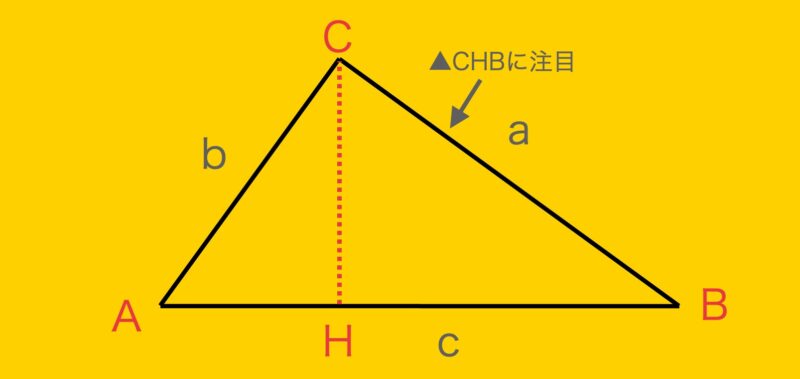
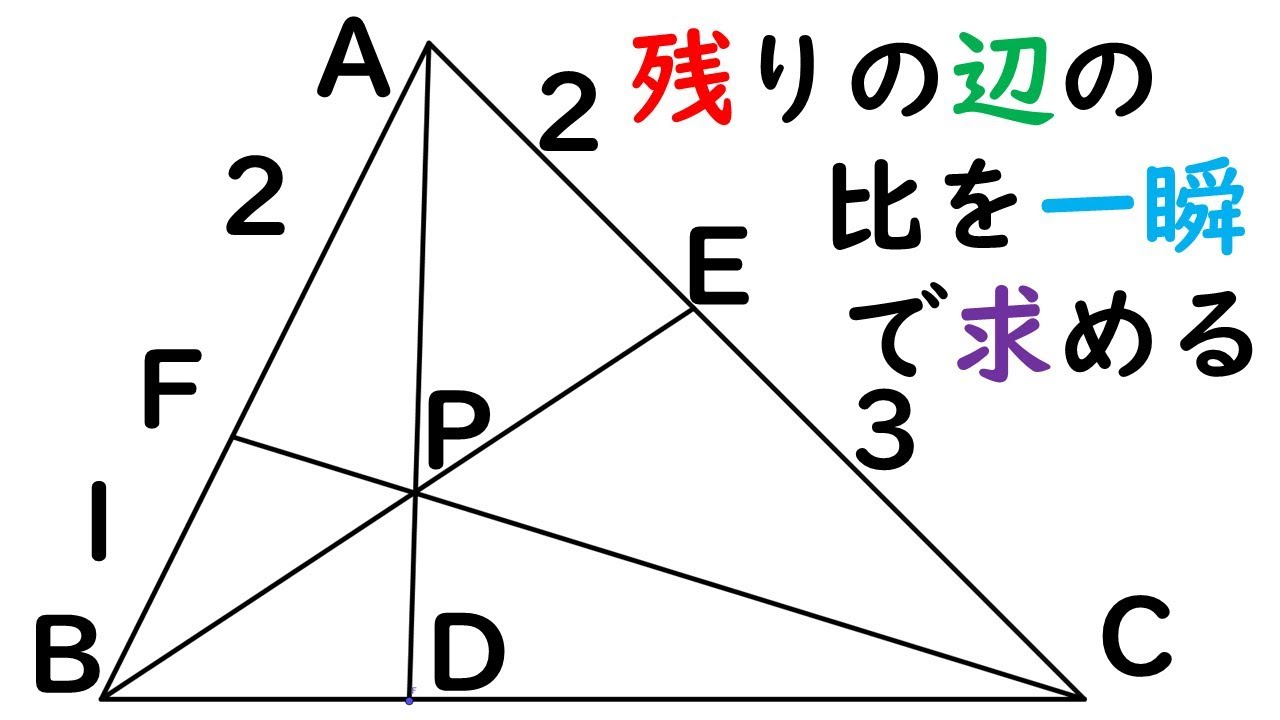
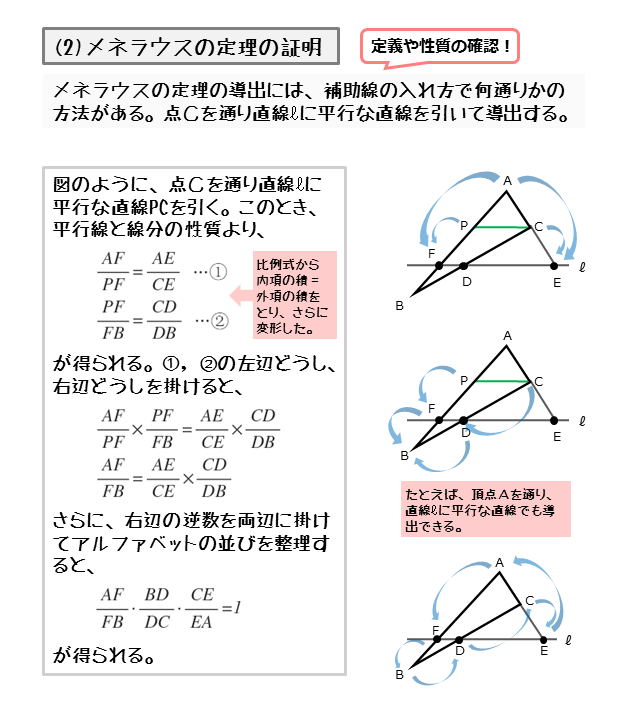
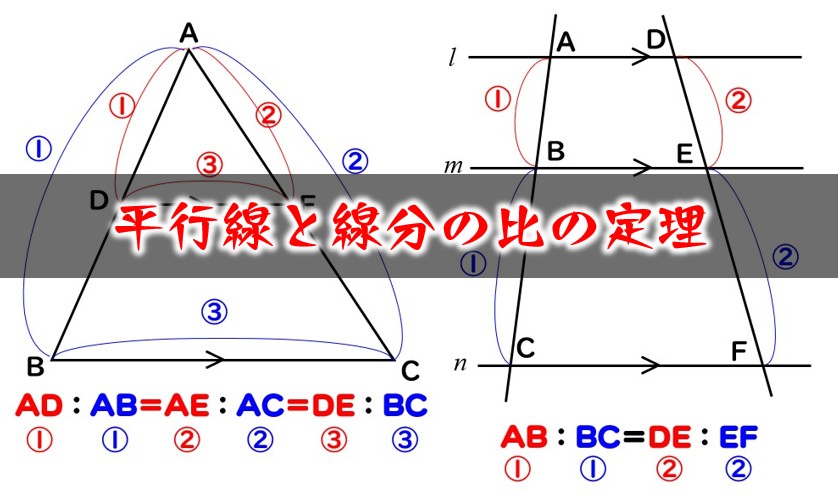
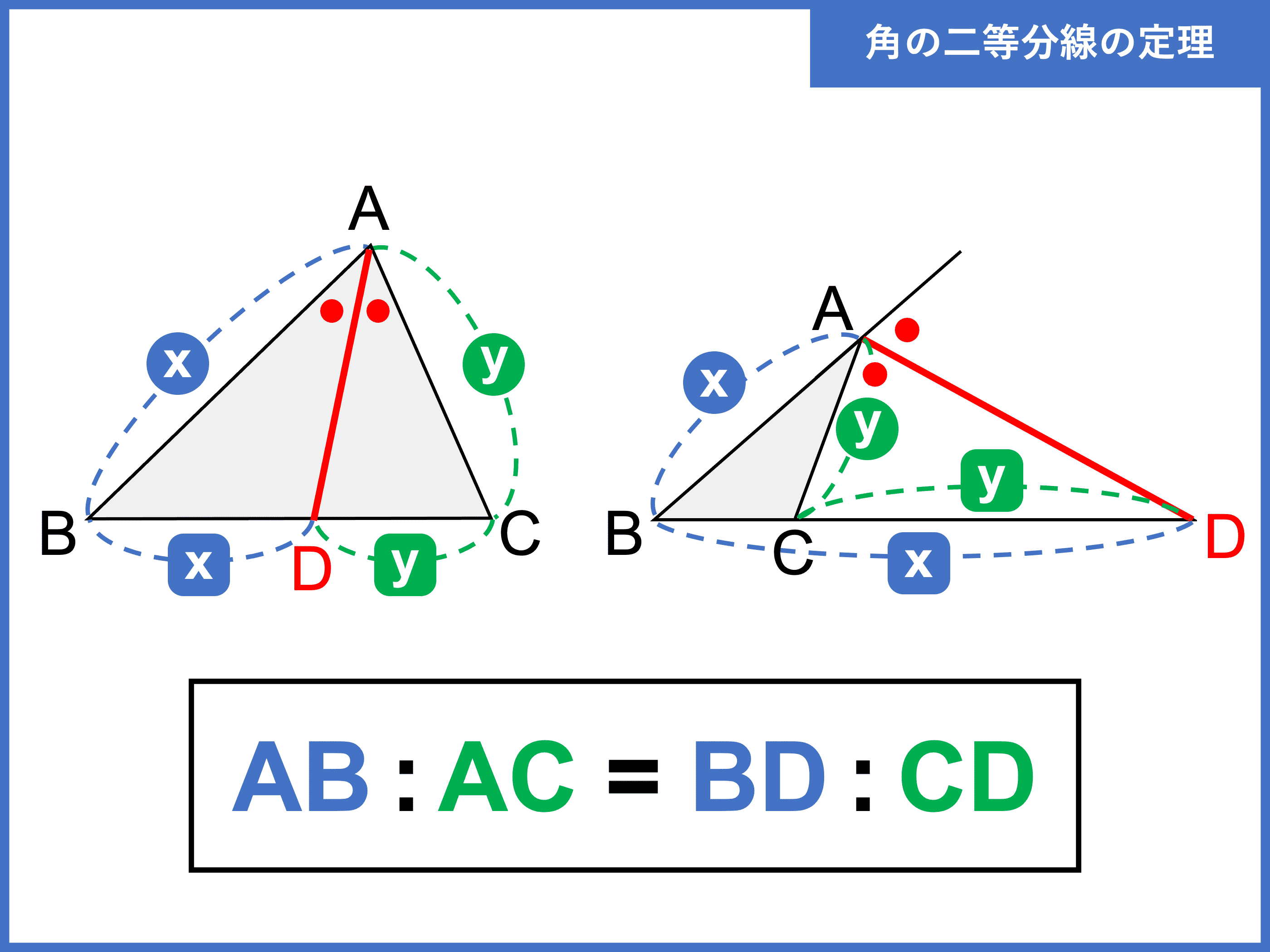
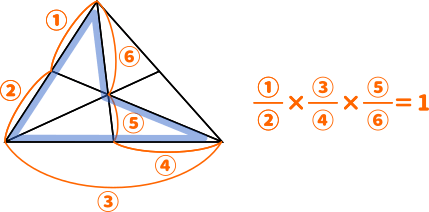
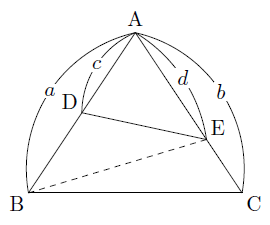
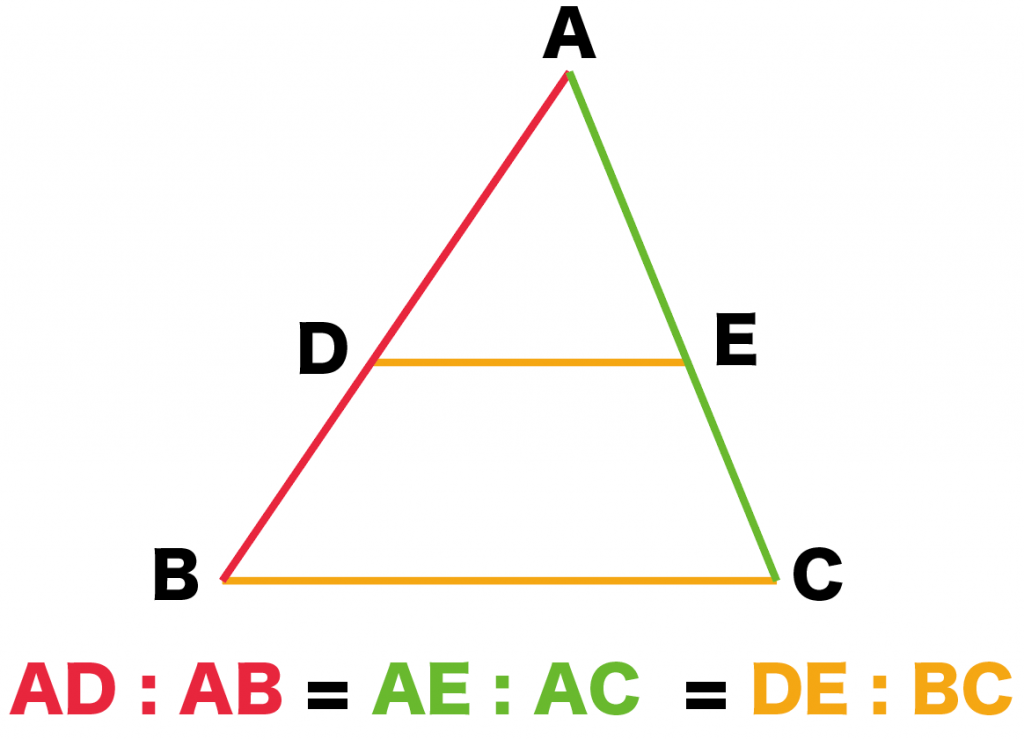
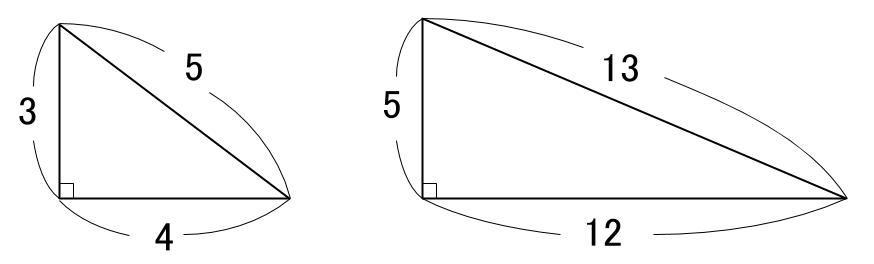
大きな三角形 ABCの 辺を対比させる」 と覚えておくと 分かりやすいと思います。 ※理由は ADEと ABCは 相似の関係になるからです。 同時に 次の比の関係 も 成り立ちます。 2つ目のパターン 2つ目の 図形のパターンは、 次のものです。 1つ目のパターンと 同じように、 前提として直角三角形においては三平方の定理が成り立つため,3つの角が30°,60°,90°である直角三角形と,45°,45°,90°である直角三角形の3辺の長さには,それぞれ次のような関係が成り立っています。 特別な直角三角形の3辺の比 30°,60°,90°の 直角三角形 45°,45°,90°の 直角三角形 3辺の比は となります。 3辺の比は
Incoming Term: 三角形 辺の比 定理,
コメント
コメントを投稿